最高3倍无损提速！数学规划求解器效率升级，论文已中顶刊TPAMI

最高3倍无损提速，用数学规划求解器寻找最优解更快了！

近日，中科大王杰教授团队（MIRA Lab）和华为诺亚方舟实验室（Huawei Noah’s Ark Lab）联合提出了分层序列/集合模型，并开发了基于该分层模型的智能决策训练方法。

显著提升混合整数线性规划（MILP）求解器求解效率，取得最高3倍无损提速。

数学规划求解器因其重要性和通用性，被誉为运筹优化领域的“光刻机”。

其中，MILP求解器是数学规划求解器的关键组件，可建模大量实际应用。

打个比方，MILP求解器就像一个智能助手，能通过数学方法和算法帮助寻找最优解。

在更复杂的情况下，比如物流调度、生产计划、金融投资等领域，MILP求解器可以帮助决策者在复杂约束条件下做出最优选择。

目前论文发表在人工智能顶级期刊IEEE TPAMI 2024。

背景与问题介绍

割平面（cutting planes, cuts）在加速求解混合整数线性规划（MILP）问题中发挥着至关重要的作用。自上世纪50年代以来，割平面法作为求解MILP问题的强大工具，已成为学术界和工业界广泛研究的重点。经过多年的实践验证，割平面法已被公认为快速求解MILP问题的关键技术。

其中割平面选择（cut selection）目标是：

选择待选割平面的恰当子集以无损提高求解MILP的效率。

据介绍，割平面选择在很大程度上取决于两个子问题：

• (P1) 应优先选哪些割平面

• (P2) 应选择多少割平面

研究人员认为，尽管许多现代MILP求解器通过手动设计的启发式方法来处理 (P1) 和 (P2)，但机器学习方法有潜力学习更有效的启发式方法。

然而，许多现有的学习类方法侧重于学习应该优先选择哪些割平面，而忽略了学习应该选择多少割平面。

此外，研究人员从大量的实验结果中发现又一子问题对求解MILP的效率有重大影响。

• (P3) 应该优先选择哪种割平面顺序

针对上述挑战，研究人员提出了一种新的分层序列/集合模型(Hierarchical Sequence/Set Model,HEM++)，并构建了基于该模型的强化学习框架来学习割平面选择策略。

下面具体展开。

割平面介绍

混合整数线性规划（MILP）是一种可广泛应用于多种实际应用领域的通用优化模型，例如供应链管理、排产规划、规划调度、工厂选址、装箱问题等。

标准的MILP具有以下形式：

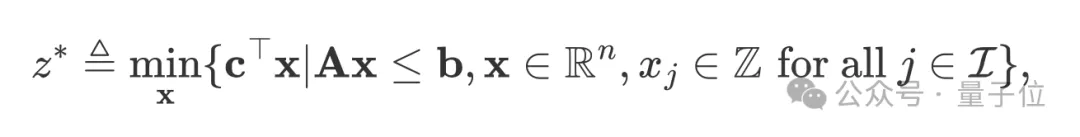
给定上述问题，丢弃其所有整数约束，可得到线性规划松弛（linear programming relaxation，LPR）问题，它的形式为：

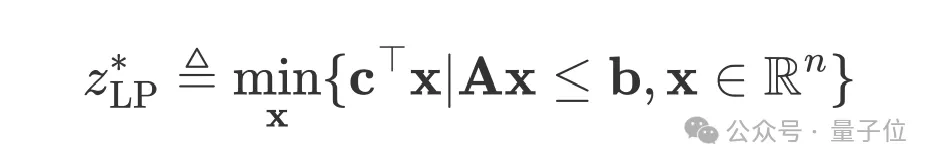
由于松弛问题扩展了原始问题的可行域，因此可有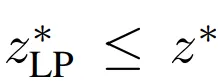，即LPR问题的最优值是原MILP问题的下界。

给定松弛问题，割平面是一类合法线性不等式，这些不等式在添加到线性规划松弛问题中后，可收缩LPR问题中的可行域空间，且不去除任何原MILP问题中任何整数可行解。

割平面选择介绍

MILP求解器在求解MILP问题过程中可生成大量的割平面，且生成的割平面会在连续的回合中不断向原问题中添加割平面。

具体而言，每一回合中包括五个步骤：

• (1) 求解当前的LPR问题；

• (2) 生成一系列待选割平面；

• (3) 从待选割平面中选择一个合适的子集；

• (4) 将选择的子集添加到(1)中的LPR问题，以得到一个新的LPR问题；

• (5) 循环重复，基于新的LPR问题，进入下一个回合。

将所有生成的割平面添加到LPR问题中可最大程度地收缩该问题的可行域空间，以最大程度提高下界。

然而，添加过多的割平面可能会导致问题约束过多，增加问题求解计算开销并出现数值不稳定问题。

因此，研究者们提出了割平面选择，它的目标是选择候选割平面的适当子集，以尽可能提升MILP问题求解效率。

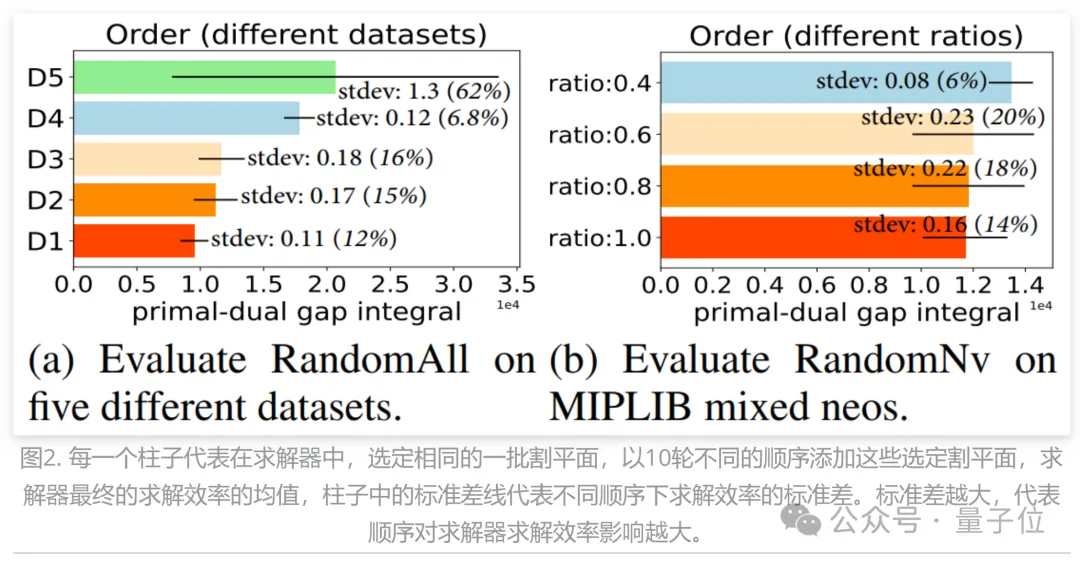
启发实验：割平面添加顺序

研究人员设计了两种割平面选择启发式算法，分别为RandomAll和RandomNV（详见原论文第3章节）。

它们都在选择了一批割平面后，以随机顺序将选择的割平面添加到MILP问题中。

结果显示，选定同一批割平面的情况下，以不同的顺序添加这些选定割平面对求解器求解效率有极大的影响（详细结果分析见原论文第3章节）。

方法介绍

据介绍，在割平面选择任务中，应该选择的最优子集是不可事先获取的。

不过，研究人员可以使用求解器评估所选任意子集的质量，并以此评估作为学习算法的反馈。

因此，团队利用强化学习（Reinforcement Learning, RL）范式来试错学习割平面选择策略。

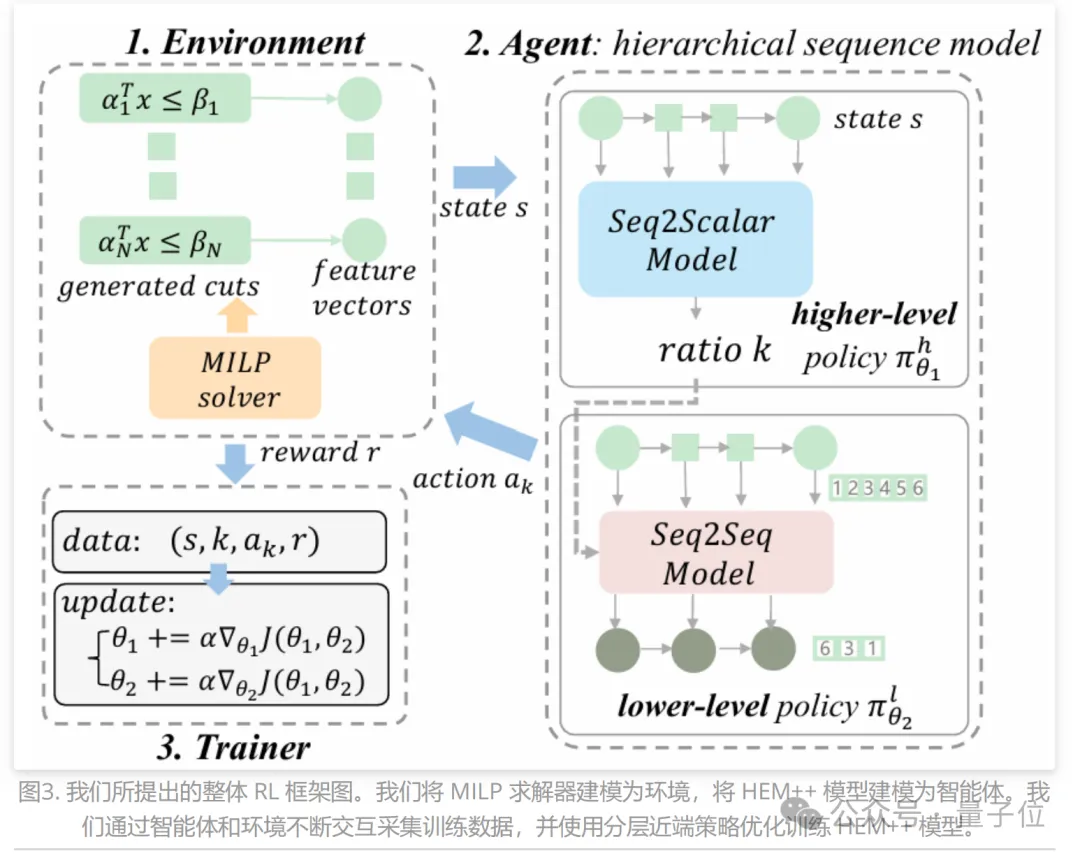
研究人员详细阐述了提出的RL框架。（整体的RL框架图如图2所示）

首先，他们将割平面选择任务建模为马尔科夫决策过程（Markov Decision Process, MDP）。

然后，详细介绍了提出的分层序列/集合模型HEM++。

最后，推导可高效训练HEM++ 的分层近端策略优化（hierarchical proximal policy optimization, HPPO）方法。

下面一一展开。

问题建模：序列决策建模

状态空间：由于当前的LP松弛和生成的待选cuts包含割平面选择的核心信息，研究人员通过（𝑀_𝐿𝑃，𝐶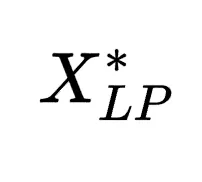，）定义状态s。

这里𝑀_𝐿𝑃表示当前LP松弛的数学模型，𝐶表示候选割平面的集合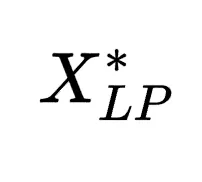，表示LP松弛的最优解。

为了编码状态信息，研究人员根据（𝑀_𝐿𝑃，𝐶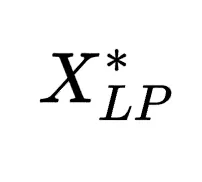，）的信息为每个待选割平面设计13个特征。

也就是说，通过一个13维特征向量来表示状态s。（具体细节请见原文第5和第6章节）

动作空间：为了同时考虑所选cut的比例和顺序，研究人员以候选割平面集合的所有有序子集构成的集合𝐴和选择cut的比例空间[0,1]的直积，即动作空间𝐴^HEM++=𝐴 x [0,1]。

奖励函数：为了评估添加cut对求解MILP的影响，可通过求解时间，原始对偶间隙积分（primaldual gap integral），对偶界提升（dual bound improvement）。

转移函数：转移函数给定当前状态s和采取的动作𝑎，输出下一状态s^’。割平面选择任务中转移函数隐式地由求解器提供。

更多建模细节请见原文第5和第6章节。

策略模型：分层序列/集合模型

如图所示，研究人员将MILP求解器建模为环境，将HEM++建模为智能体，下面详细介绍所提出的HEM++模型。

可以看出，HEM++由上下层策略模型组成。上下层模型分别学习上层策略（policy）π^ℎ和下层（policy）π^𝑙。

首先，上层策略通过预测恰当的比例来学习应该选择的cuts的数量。

假设状态长度为N，预测比率为k，那么预测应该选择的cut数为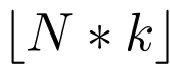，其中表示向下取整函数。

研究人员定义。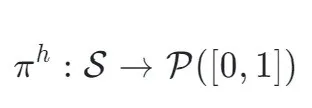

其次，下层策略学习选择给定大小的有序子集。

下层策略可以定义 S x [0，1] → P（𝐴），其中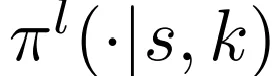表示给定状态s和比例k的动作空间上的概率分布。

具体来说，研究人员将下层策略建模为一个序列到序列或者集合到序列模型（sequence/set to sequence model, sequence/set model）。

最后，通过概率乘法定理可得分层cut选择策略，即：。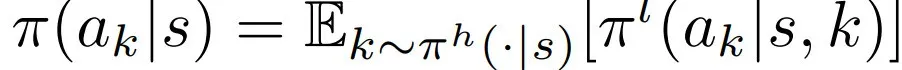

训练方法：分层近端策略优化方法

研究人员用[0，1] x 𝐴 表示动作空间，用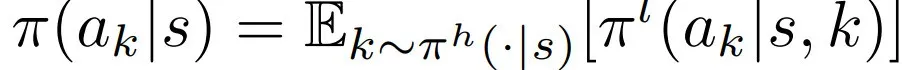表示分层割平面策略。

最终推导出HPPO，当前策略和旧策略的概率比表示如下：

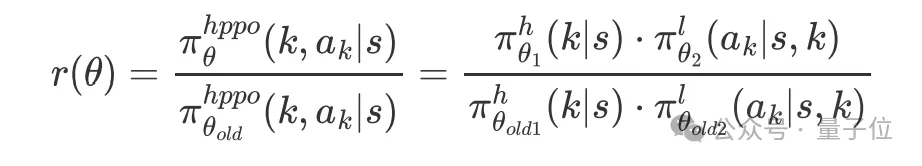
为了避免过大的策略更新，研究人员对此概率比进行裁剪得到r^clip。

进一步地，给定优势函数的估计器，优化目标为：

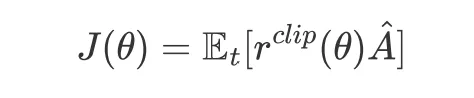
最后，分层策略梯度如下：

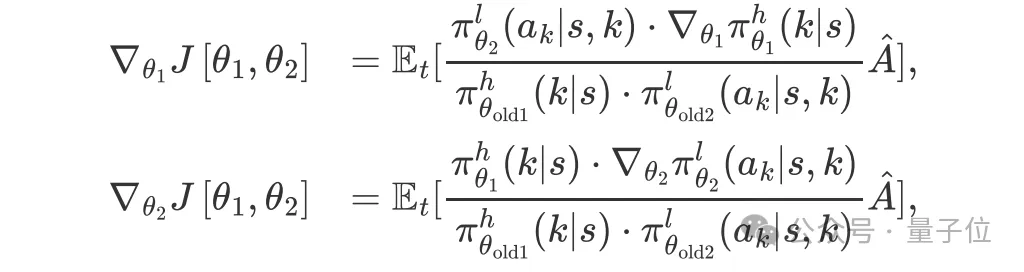
具体细节请见原文第6章节。

实验介绍

实验共有五个主要部分。

• 实验1. 在3个人工生成的MILP问题和来自不同应用领域的6个具有挑战性的MILP问题基准上评估新方法；

• 实验2. 进行消融实验，以提供对HEM++的深入洞察；

• 实验3. 测试HEM++针对问题规模的泛化性能；

• 实验4. 可视化新方法与基线所选择的割平面特点；

• 实验5. 将新方法部署到华为实际的排产规划问题中，验证HEM++的优越性；

下面仅简单介绍下实验1，更多实验结果，可参见原论文第8章节。

研究人员提醒道，论文中汇报的所有实验结果都是基于PyTorch版本代码训练得到的结果。

如图所示，在多个开源数据集和工业数据集上对比了HEM++和最先进开源求解器SCIP基线。

实验结果显示，HEM++可在保持求解精度不变的情况下，大幅提升求解效率。

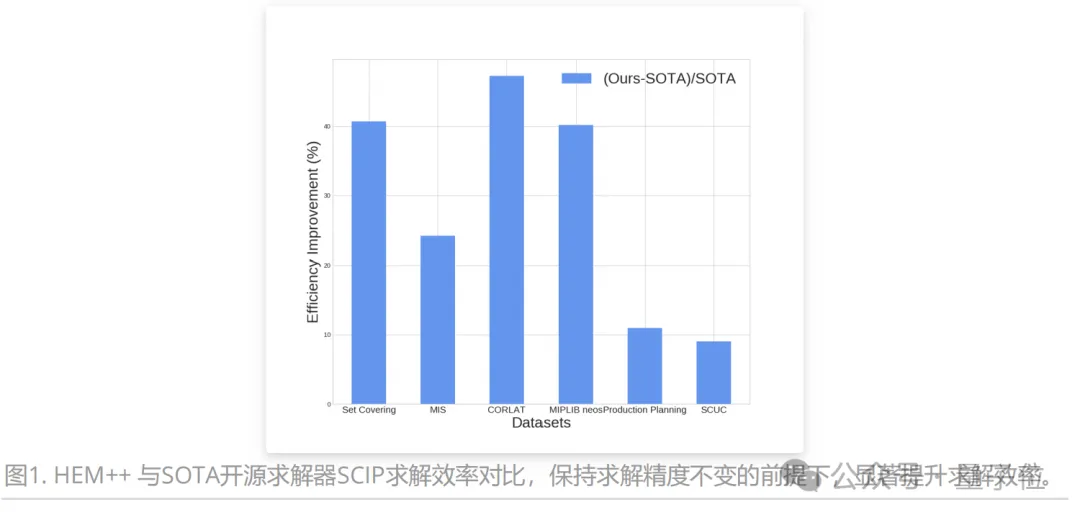
据团队介绍，相关技术和能力整合入华为天筹（OptVerse）AI求解器，助力提升天筹AI求解器竞争力，成为其首批关键AI特性。

天筹AI求解器将运筹学和AI相结合，针对线性和整数模型寻找最优解，以通用形式描述问题，高效计算最优方案，助力企业量化决策和精细化运营。

天筹AI求解器曾获世界人工智能大会最高奖“卓越人工智能引领者” SAIL奖，并在国际权威数学优化求解器榜单中的5项重量级榜单登上榜首。

相关算法整合入华为MindSpore ModelZoo模型库，助力国产开源生态。

华为MindSpore是一个全场景深度学习框架，目标是实现易开发、高效执行、全场景覆盖三大目标。

更多细节欢迎查阅原论文。

本论文作者王治海是中国科学技术大学2020级硕博连读生，师从王杰教授，主要研究方向为强化学习与学习优化理论及方法，人工智能驱动的芯片设计等。他曾以第一作者在TPAMI、ICML、ICLR、AAAI等顶级期刊与会议上发表论文六篇，一篇入选ICML亮点论文（前3.5%），曾获华为优秀实习生（5/400+）、国家奖学金等荣誉。

华为MindSpore ModelZoo模型库：https://gitee.com/mindspore/models/tree/master/research/l2o/hem-learning-to-cut

论文地址：https://ieeexplore.ieee.org/document/10607926
代码地址：https://github.com/MIRALab-USTC/L2O-HEM-Torch
数据地址：https://drive.google.com/drive/folders/1LXLZ8vq3L7v00XH-Tx3U6hiTJ79sCzxY
会议版本论文（ICLR 2023）：https://arxiv.org/abs/2302.00244