推荐系统自1992 年代诞生以来, 到2024 年的今天已经有32 年的发展历程。在这几十年的发展历程中,各个互联网和科技公司上线过数以百万计的推荐系统模型。尽管推荐系统经历过 2012 到 2014 年的发展低潮,但很快就被后起之秀快手和字节跳动一改颓势,从而重新成为了热点技术。在经历过浅层学习和深度学习之后,推荐系统的研究方向目前在往多元化方向发展,包括公平性和序列推荐等等。
推荐系统的经典算法非常多,从早期的浅层学习算法协同过滤,到矩阵分拣和线性模型,再到后面的深度学习和序列推荐,每一个发展时期都见证了某几个里程碑算法赢家通吃的现象。推荐系统的技术这么成熟,还会有什么我们平常不留心的知识吗?你别说,还真有。不信请看本文:
1、什么?协同过滤算法在我的数据集合上有可能不成立?
是的,有可能。在 2023 年召开的国际学术会议 CECNet 2023 上,研究人员发表了一篇题为 “Collaborative Filtering is a Lie or Not ? It Depends on the Shape of Your Domain” 的论文。这篇论文指出,协同过滤在某些数据集合上可能不成立。
作者首先利用任意一种降维算法,使用相似度矩阵推导的距离矩阵将用户-用户关系映射到二维空间。然后定义点i指向点 j 方向的向量为(Sim(i,j)-C, Sim(i,j)-C), 其中 Sim(i,j) 为用户 i 和用户 j 之间的相似度,而 C 为任意实数。
为了使向量场成立,我们这个虚拟的向量场非对称化,也就是:本来点 i 到点 j 的向量和点 j 到点 i 的向量是一样的,但这是不成立的向量场,因此我们强制它们符号相反,构造一个合法的向量场。
我们根据推荐系统的预测评分是实数的特点,认为在这些离散点之间存在着许多其他点,使得我们定义的向量场成立。
根据 Poincare-Hopf Theorem ,如果一个向量场是定义在一个有向和紧致的流形上时,这个向量的零点的数量只和流形本身的欧拉示性数有关,而向量场本身无关。所以,如果我们降维下来的这个二维空间数据集合,满足特定性质,则协同过滤算法是不成立的。意不意外?惊不惊喜?
2、什么?矩阵分解算法中的先验概率不是高斯分布?
是的,矩阵分解算法中的先验概率不是高斯分布,是锥形分布。
研究人员在国际学术会议 CAMMIC 2023 上发表了一篇题为 “Analysis and visualization of the parameter space of matrix factorization-based recommender systems”的论文,对矩阵分解算法中的用户向量矩阵和物品向量矩阵进行了 Henze-Zirkler 检验,发现矩阵分解算法中用户向量和物品向量的先验分布不是高斯分布。作者随后把这些向量进行了可视化,得到了下图:
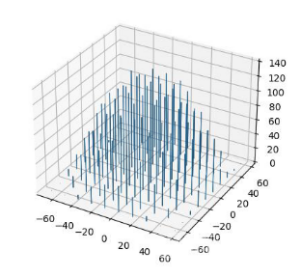
图 1 用户向量分布
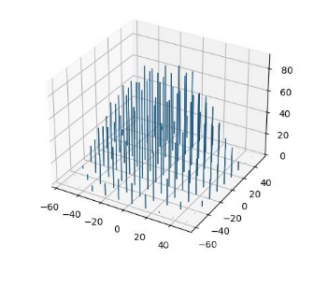
图 2 物品向量分布
通过观察可视化结果,并通过逻辑分析,我们得到如下结论:矩阵分解算法中的先验概率是锥形分布,不是高斯分布。
3、什么?推荐系统评分数据的长尾现象可以用泊松过程建模?
是的,可以。我们可以通过如下关系对推荐系统的用户评分进行建模,我们姑且称它为推荐系统中的齐夫分布:
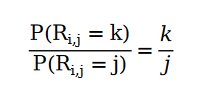
打个比方。在电影评分网站中,口碑 5 星的电影的评分数量为 5;口碑 4 星的电影的评分数量为 4 …… 我们发现,如果我们用Non-homogeneous Poisson Process 给用户打分行为进行建模之后,能够通过解方程的形式得到符合评分满足齐夫分布的解。
在 2023 年召开的国际学术会议 CAMMIC 2023 上,研究人员发表了一篇题为 “Evolution of the Online Rating Platform Data Structures and its Implications for Recommender Systems”,详细叙述了这一建模过程。
4、什么?推荐系统可以完全不利用任何数据解决冷启动问题?
推荐系统中的冷启动问题一直是个老大难问题。传统的解决方案无外乎 Transfer Learning / Meta Learning 或者热点推荐。但是从 2021 年开始到 2023 年出现了一系列的无需 Transfer Learning / Meta Learning 解决推荐系统冷启动的零样本学习算法:ZeroMat、DotMat、RankMat、PoissonMat 和LogitMat。这些算法,无一例外的都不需要使用任何数据,就能取得比肩使用全量数据的矩阵分解算法的效果。
下面我们看两张来自 LogitMat 原始论文的实验数据(MovieLens 1 Million Dataset)图片:
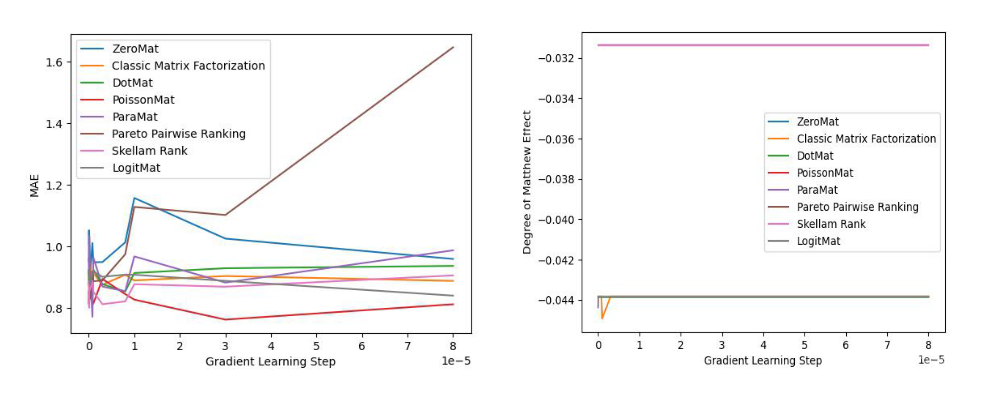
图 3 MAE 对比实验
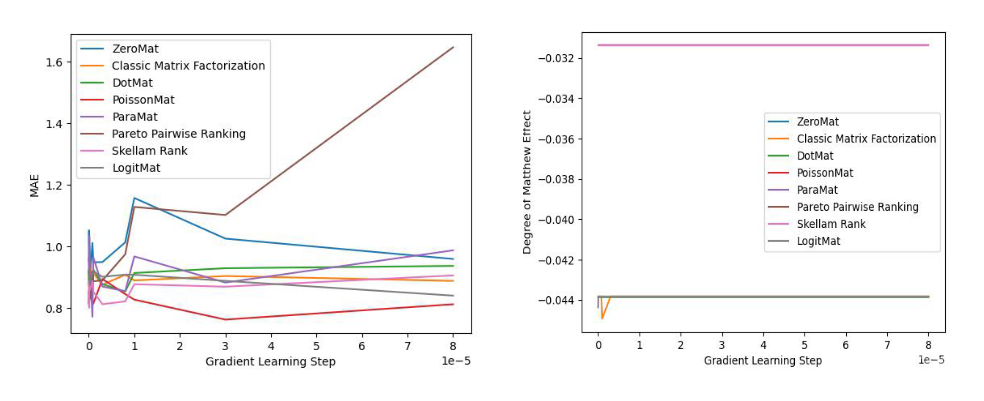
图 4 公平性对比实验
通过观察实验结果,我们发现这些算法无一例外的都可以比肩全样本算法,甚至取得更好的效果。
5、什么?矩阵分解+正则化可以在 MovieLens 数据集上做到 MAE 0.6?
是的,可以。推荐系统的从业人员特别喜欢用 MovieLens 数据集测试自己的算法,然而历史上的算法的 MAE 值通常都在 0.7 和 0.8 之间。其实,只要通过更改一下正则化项的惩罚函数的定义方式,就可以将 MAE 降到 0.6。下面我们来看一下研究人员是怎样通过更改正则化项来优化矩阵分解算法的:
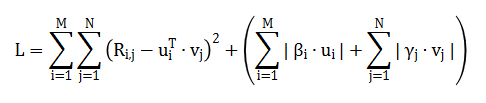
通过随机梯度下降对损失函数 L 求解,得到如下公式:
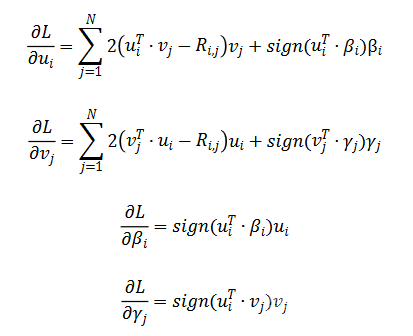
我们通过在 MovieLens Small Dataset 上做实验,发现通过修改矩阵分解的正则化项,可以将 MAE 降到 0.62 :
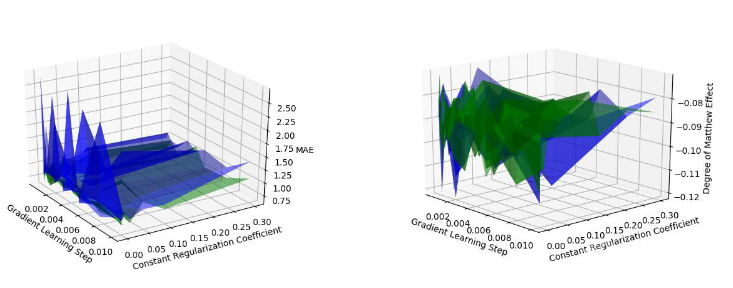
图 3 MAE 对比实验图 4 公平性对比实验
关于正则化的这项新技术,可以参考学术论文 Theoretically Accurate Regularization Technique for Matrix Factorization based Recommender Systems 。
6、什么?推荐系统的结果还可以这样可视化?
是的,我们可以对推荐系统进行可视化。我们这里只举一个例子:Takens Embedding。Takens Embedding 的细节我们不在这里叙述,我们这里只给出三张图片,为读者演示一下如何利用 Takens Embedding 对推荐系统 MAE 曲线进行升维,以便对推荐系统进行可视化。具体的技术细节,可以参考学术论文 Effective Visualization and Analysis of Recommender Systems。
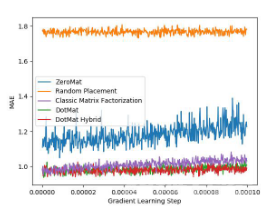
图 5 MAE @ 1D
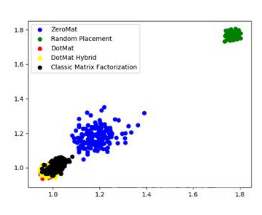
图 6 MAE @ 2D
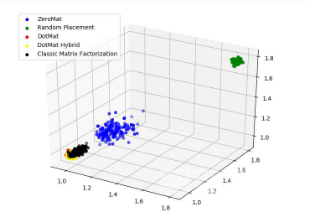
图 7 MAE @ 3D
图5、图6 和 图7展示了 MAE 曲线在 1D、2D 和 3D 空间的不同情况。2D 和 3D 空间的误差点云可以更好的反映 MAE 的具体情况。
尽管推荐系统发展了许多年,但是我们每天仍然面临着许多新的挑战,仍然有数不胜数的新技术和新产品不断出现,冲击着我们的知识体系。因此,我们需要时刻保持着一颗年轻的和求知若渴的心态,这样才能让我们在时代的大潮中保持着不败的竞争优势。
作者介绍
汪昊,前 Funplus 人工智能实验室负责人。曾在 ThoughtWorks、豆瓣、百度、新浪等公司担任技术和技术高管职务。在互联网公司和金融科技、游戏等公司任职 12 年,对于人工智能、计算机图形学和区块链等领域有着深刻的见解和丰富的经验。在国际学术会议和期刊发表论文 42 篇,获得IEEE SMI 2008 最佳论文奖、ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 最佳论文报告奖。






还没有评论,来说两句吧...