看不懂新开源的DS-Prover V2版本？解读来了，攻克像人类一样数学证明，达到SoTA水平，不知道如何测？样题来了

五一凌晨，DeepSeek终于更新了新开源的 DeepSeek-Prover V2的自述文件。速览一下：

- 解决近 90% 的 miniF2F 问题（88.9%）

- 显著提高 PutnamBench 上的 SoTA 性能

- 在正式版本中对 AIME 24 和 25 问题取得了惊艳的通过率

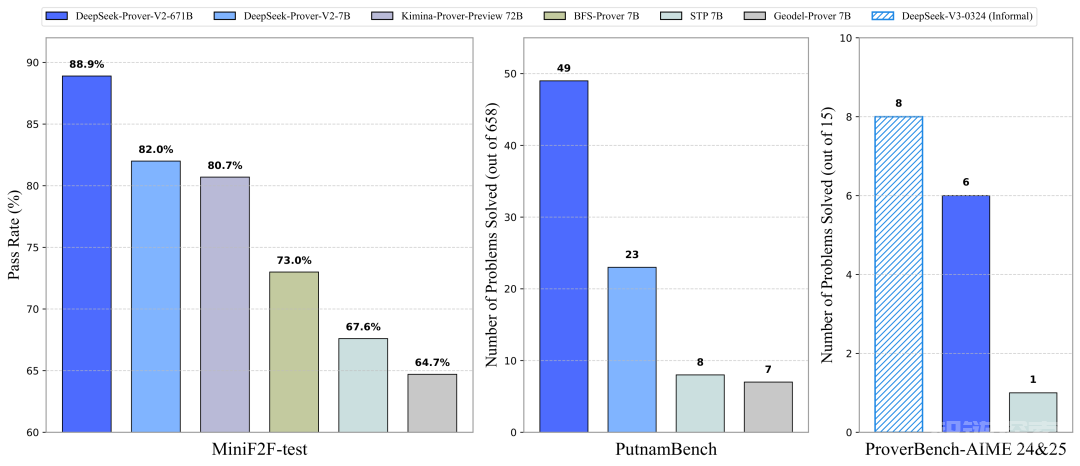
点评：亮点上来看，DeepSeek-Prove V2模型在死磕LLM在推理数学问题上能给出答案但却给不出严格正确的推理步骤的问题。而且在一中先进模型中达到了SoTA的水平，图四是前十榜单。

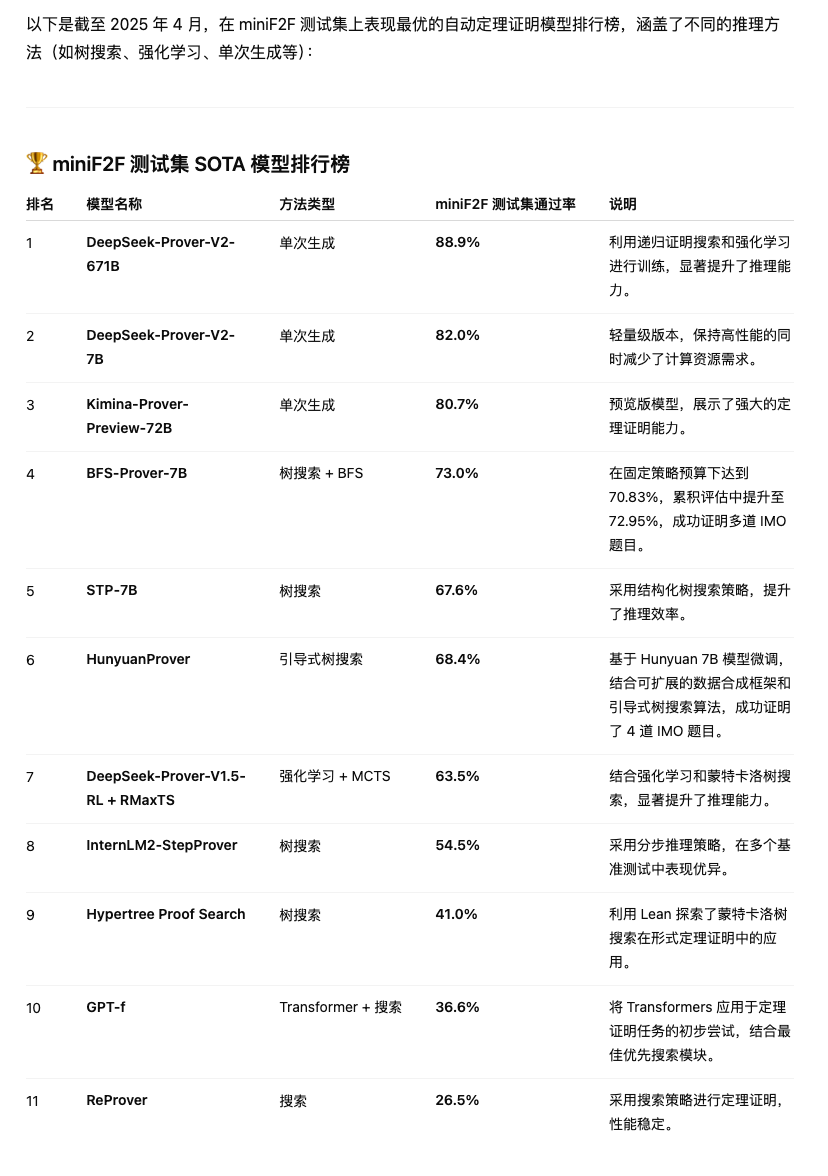
AIME这个测试集大家很清楚了，这里不再赘述。这里重点科普下miniF2F测试。

miniF2F 是什么？

miniF2F 是一个面向大型语言模型（LLM）数学推理能力评测的基准数据集，全名是 mini Formal to Formal。它源自更早的 F2F（Formal-to-Formal） 项目，但体量更小，便于在不同模型上快速评测。

它是一组高中及大学初等数学题目，覆盖以下领域：代数、数论、微积分、几何、离散数学等等。这些题目用自然语言表述（类似“证明对于任意正整数n，有…”），目标是评测 LLM 能否像人类数学家一样，通过推理过程得出正式的数学证明。

举个简化版的例子，miniF2F的题目是这样的——

证明：对于任意正整数 n，2n + 1 是奇数。

LLM 要能输出严谨证明，比如：

对于任意正整数 n，有 2n 是偶数，偶数加 1 是奇数，因此 2n + 1 是奇数。

如果你做 LLM 评测、数学任务微调或者学术方向，这个数据集是很重要的 benchmark。

DS如何做到的？

DS开发了一种简单而高效的递归定理证明流程，利用V3模型作为统一工具，既用于子目标分解，也用于形式化处理，并引导V3 将定理分解为高层次的证明草图，同时在 Lean 4 中形式化这些证明步骤，从而生成一系列子目标。

使用较小的 7B 模型来处理每个子目标的证明搜索，以降低相关的计算负担。一旦复杂问题的分解步骤被解决，将完整的逐步形式化证明与 DeepSeek-V3 的相应思维链配对，创建冷启动推理数据。

想要测评或者试用的朋友可以跑起来了，当然建议跑7B模型了，671B不是一般设备能跑的。model_id = "DeepSeek-Prover-V2-7B"