大模型「强崩溃」！Meta新作：合成数据有「剧毒」，1%即成LLM杀手

1%的合成数据，就让LLM完全崩溃了？

7月，登上Nature封面一篇论文证实，用合成数据训练模型就相当于「近亲繁殖」，9次迭代后就会让模型原地崩溃。

论文地址：https://www.nature.com/articles/s41586-024-07566-y

然而，许多大佬都不同意这篇文章的方法和结论。

比如，Scale AI的CEO Alexandr Wang就很看好合成数据的前景，英伟达发布的开源模型Nemotron-4 340B甚至使用了98%的合成数据。

最近，Meta、纽约大学、UCLA机构发表的最新论文，再一次动摇了这些大佬们的结论。

论文地址：https://arxiv.org/abs/2410.04840

他们发现，即使合成数据仅仅占到总数据集的最小部分，甚至是1%的比例，仍然可能导致模型崩溃。

甚至，ChatGPT和Llama这种较大的模型，还可能放大这种「崩溃」现象。

强模型崩溃，如何发生的？

随着越来越多的合成数据出现在训练集中，一种新的现象应运而生：「模型崩溃」。

所谓「模型崩溃」，是指随着时间的推移，LLM或大型图像生成器在其前几代生成的数据上进行递归训练，导致性能下降，直至模型完全丧失能力的情况。

围绕着这个问题，AI学界和业界的大佬依旧莫衷一是，尚未达成一致的结论。

而合成数据究竟会在多大比例、多大程度上导致「模型崩溃」，直接影响着我们在未来如何应用这项技术。

从直觉上理解，合成数据导致「模型崩溃」的底层逻辑，是由于模型开始对合成数据中的模式进行过拟合，而这些模式可能无法代表现实世界数据的丰富性或可变性。

如果进行连续的迭代训练，这种反馈循环会导致模型强化合成数据中存在的错误、偏差或过度简化，因而损害了对现实世界的准确表示能力和泛化能力。

总体而言，这篇文章旨在回答以下两个重要问题：

Q1：模型崩溃是不可避免的，还是可以通过策略性地混合真实数据和合成数据来解决？

Q2：较大的模型比较小的模型更容易崩溃吗？

针对这两个问题，论文以经典线性设置中的回归问题为例进行了理论分析，之后在「玩具设置」（MINIST数据集+迷你模型）和更接近真实场景的GPT-2模型上运行了实验。

理论设置

数据分布

考虑从真实数据分布P_1采样得到的n_1个独立同分布样本𝒟_1={(x_i, y_i)∣1≤i≤n_1}，以及从合成数据分布采样得到了n_2个独立同分布样本𝒟_2={(x_i, y_i)∣1≤i≤n_2}，令n:=n_1+n_2为训练数据总量。

这里，数据分布的特征可以在ℝ^d×ℝ上给出，即P_k=P_{Σ_k,w_k^∗,σ_k^2}：

其中，每个Σ_k都是一个d×d的正定协方差矩阵，捕获输入特征向量x的内在变化；σ_k控制每种分布中标签噪声的水平。

为了简洁起见，我们将对w_k^∗做出以下先验假设（对于某些d×d正半定矩阵Γ和Δ）：

- 真实标签：w_1^∗∼N⁢(0,Γ)

- 真实标签与合成标签之间的不匹配：δ:=w_2^∗−w_1^∗∼N⁢(0,Δ) ，独立于w_1^∗

其中，矩阵Γ捕获真实/测试分布中的真实标签函数的结构P_1；矩阵Δ=cov⁢(w_2^∗−w_1^∗)捕获数据分布P_1和P_2之间关于条件分布p⁢(y|x)差异的协方差结构，连同标签的噪声水平σ_1^2和σ_2^2。

平均而言，两种分布的L2范数差异可以表示为，。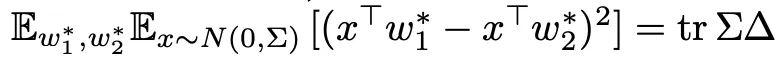

因此，合成数据的质量就可以被定义为，。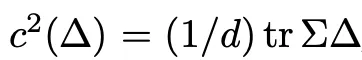

模型和性能度量

给定训练数据，模型的学习目标是构建一个估计器w\hat，这可以看作是一个线性模型 x↦x^⊤⁢w\hat。与真实数据分布P_1对比，模型的测试误差f\hat:ℝ^d→ℝ就可被定义为：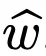

针对不同的模型，f\hat就是本篇论文的主要研究对象。此处考虑两类易于分析处理的模型：1）经典线性模型，对输入空间中的回归施加惩罚，以及2）通过随机投影得到特征空间，之后施加回归惩罚获得的模型。

第一类线性模型的优化目标如公式3所定义：

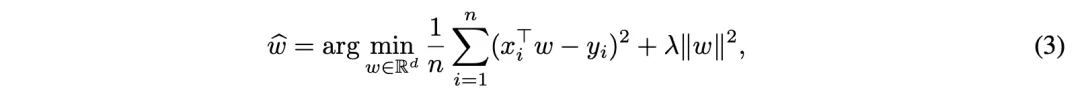
该模型存在如下的比例缩放限制（proportionate scaling limit）：

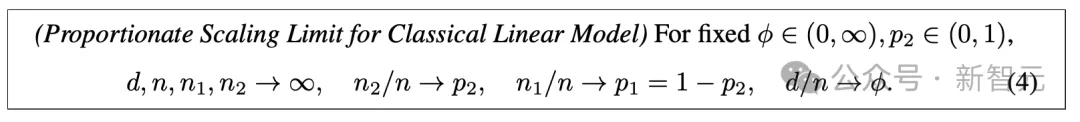
由此，我们可以得到表示经典线性模型 f_{C⁢L}\hat的定理1：

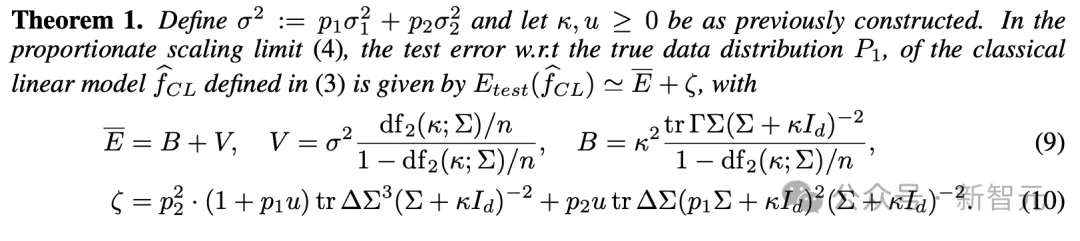
由定理1和相关推论可知，在Scaling Law范式中（ϕ→0+），如果要保持稳定，则必须要求p2→0+，即仅对真实数据进行训练，否则就会导致模型崩溃。

对第二类的随机投影模型（random projections model），可以通过其中的随机投影来简单近似神经网络。

相当于，模型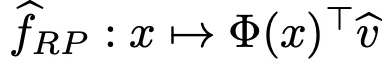中，v\hat ∈ ℝ^k通过拟合数据集进行学习，优化目标如公式5所定义：

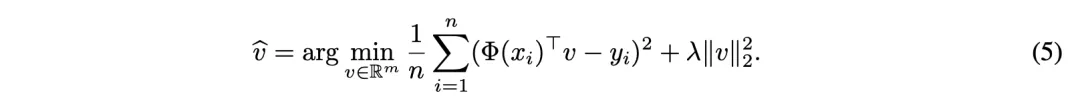
同样规定在如下的渐近（asymptotic）机制中工作：

这类模型可以被视为实际神经网络高维动态的简化。将定理1扩展到随机投影情况，可以得到定理2：

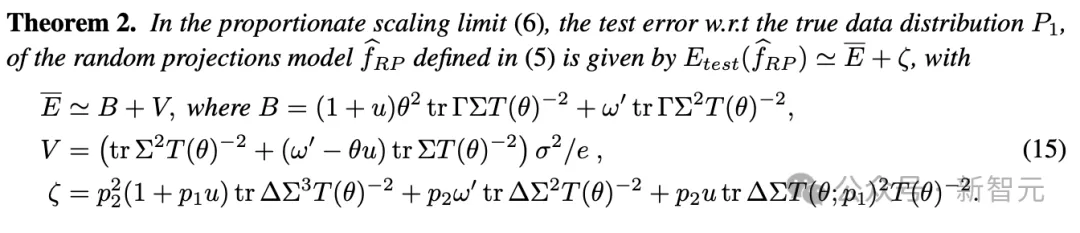
其中，ζ表达式的第一项给出了下界。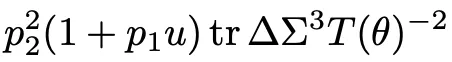

这就意味着，除非p2→0+，即训练集中合成数据部分消失，否则模型的性能将始终稳定在基线E\bar之上（意味着强烈的模型崩溃）。

此外，其中的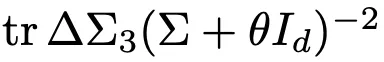部分仅取决于模型的设计选择（之前通过标量θ定义），因此可以预计，不同的设计选择（例如模型大小），将导致不同的模型崩溃轮廓。

实验结果

如上所示，定理2作为定理1的拓展，给了我们相同的结论：要想模型不崩溃，合成数据比例就需要无限接近0。

接下来，作者通过一系列实验验证了这一理论推导，并探究模型尺寸在其中扮演的作用。

图1对应的实验中，训练样本总数固定为 n=500，不同的c^2值对应不同质量的合成数据。

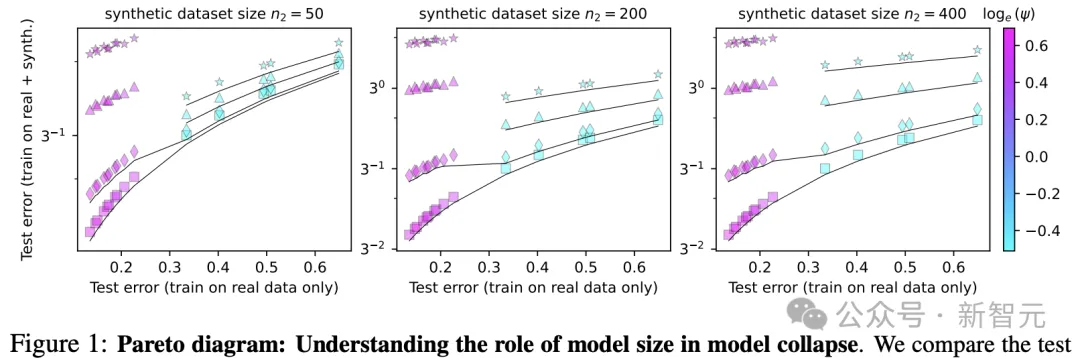
c^2=0 （非常高质量的综合数据），用方形标记表示；c^2=0.1 （高质量合成数据），用菱形表示；c^2=0.5 （低质量），用三角形表示，以及c^2=1 （非常低质量的合成数据），用星形表示

由图可知，对于较高质量的合成数据（方形和菱形），使用较大的模型（即更大的ψ）的确是最佳实践；但如果数据质量较低，模型并不是越大越好，最佳权衡反而处于中等大小。

此外，如图5所示，网络的宽度m也会造成影响，而且实验得到的曲线与理论预测值的拟合效果比较理想。

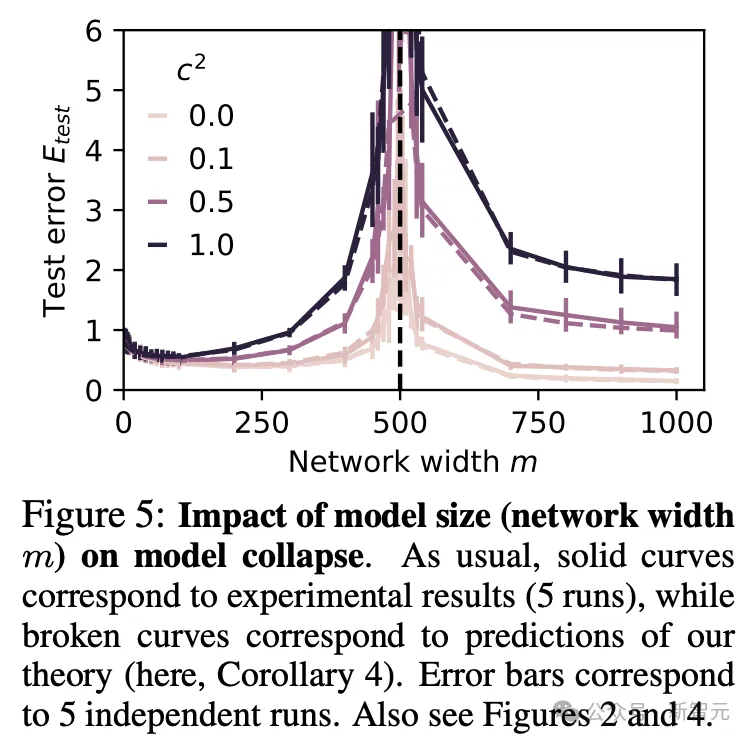
实线对应实验结果（5次运行），而虚线对应理论预测

改变合成数据的质量后，图5所示的整体趋势依旧成立。

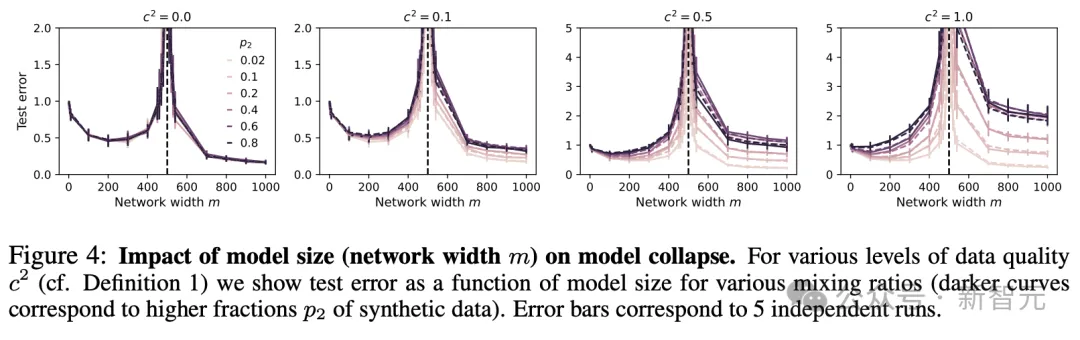
图6所示的实验采用了经过全面训练的两层网络，但仅根据合成数据进行训练，依旧支持了上述的总体趋势：

- 合成数据造成了显著的模型崩溃

- 模型越大，崩溃程度越严重

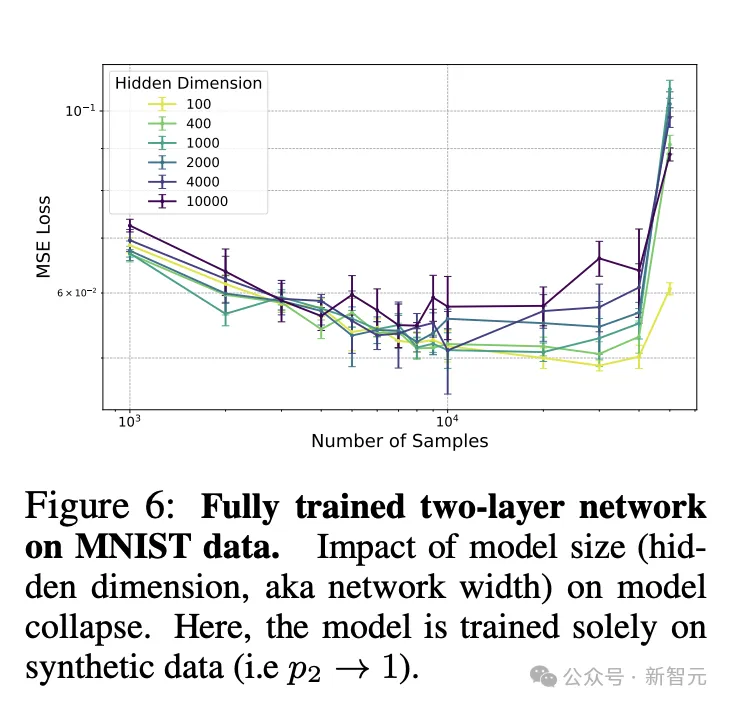
图7分别显示了随机特征模型（左）和完全训练的神经网络（右）的结果，探究合成数据比例的影响。

两种情况基本一致，除非P_2接近0，否则模型就逐渐脱离Scaling Law的轨迹，逐渐拉平成为一条水平线，即MSE损失不再随样本增加而降低，意味着出现了模型崩溃。

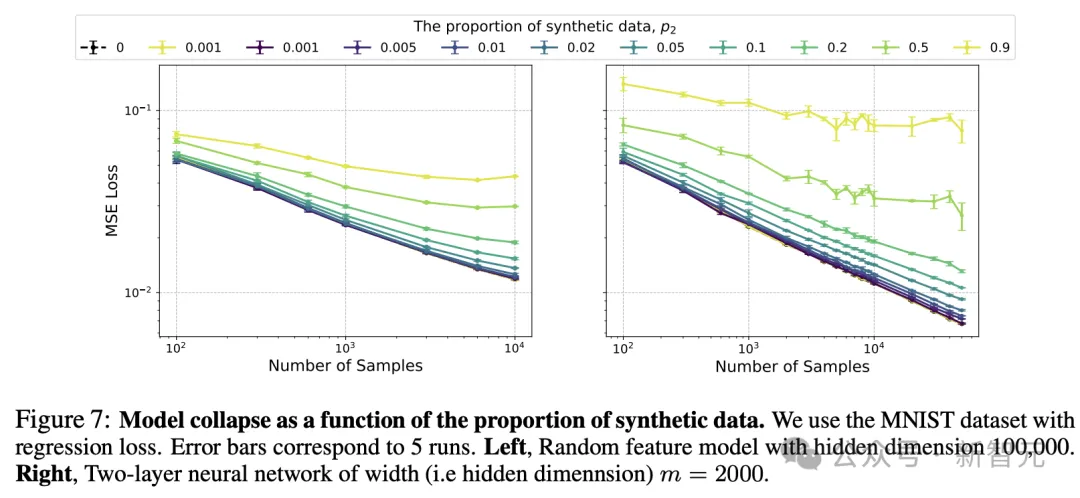
相比图7的小模型和小数据集，图8使用的BabiStories数据集和GPT-2模型更接近现实中的复杂情况。

可以看到，即便是少量的合成数据也会延迟Scaling Law的进展，作者预计，这最终会导致最终Scaling Law提前达到饱和状态或至少出现非常糟糕的指数（即小指数）。

图8（右）所示的关于模型尺寸的影响。在数据集的某个阈值前，较大/较深的模型保持较低的测试损失；但超过一定阈值后，较小的模型反而由于减少过拟合而占了上风。

这表明，较大的模型往往会将模型崩溃放大到某个插值的阈值之外。

BabiStories包含Mixtral-8x7B生成的高质量合成数据

数据混合，能否防止LLM崩溃？

如上，作者分别从理论、实证上，证实了强模型崩溃所在。

接下来，他们将通过合成数据策略，探索如何缓解模型崩溃这一现象。

这里首先假设有关于数据源的明确信息，并使用两种数据混合方法：

1 加权数据混合

2 战略性迭代混合

加权单步数据混合

为了研究学习真实数据和替代数据（例如合成数据）混合的scaling law，考虑的设置需包括以下优化问题：

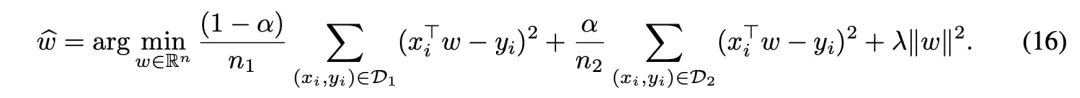
结果如下所示，真实数据+模拟数据混合法，无法解决模型崩溃问题。

在实验中，作者使用了多个不同的真实数据n1和合成数据n2的大小值。

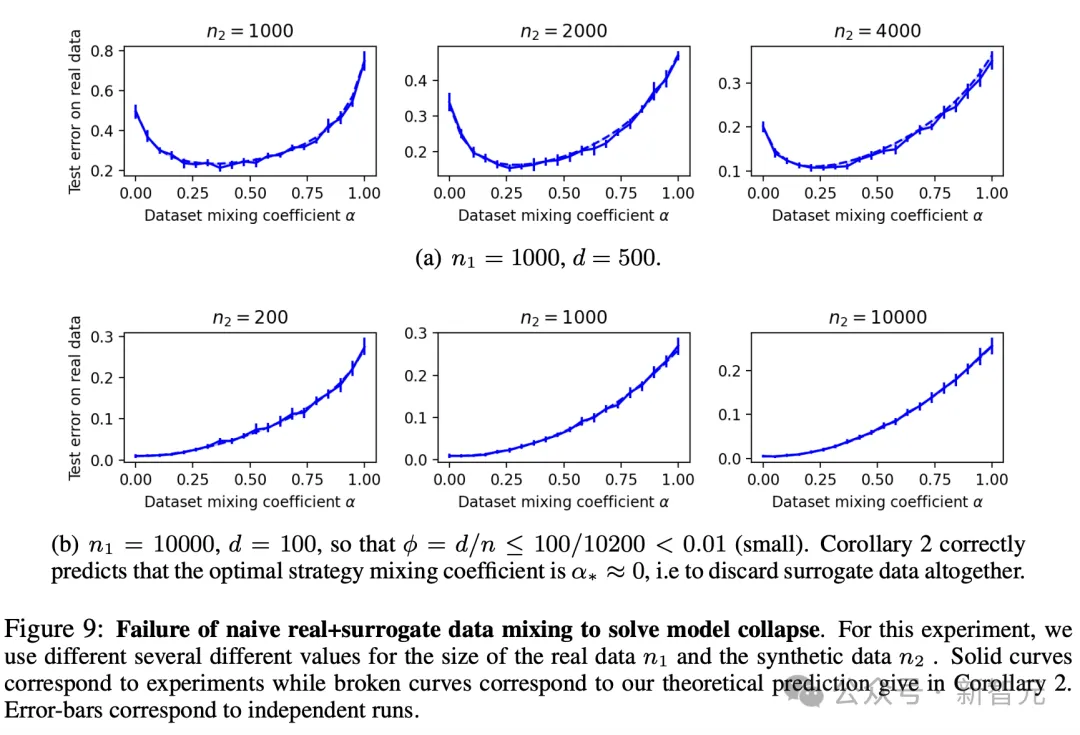
动态/多步数据混合

迭代混合恢复了scaling law，但在实践中可能不可行。

研究人员观察到，在t次迭代（t的数量级为log(n/d)）的迭代混合后，会得到与E成比例的缩放规律，这在图10中得到了经验证实。

然而，这需要付出显著的自举（bootstrapping）成本，大量的真实数据，以及在多次迭代中清晰区分真实和合成数据的能力——这些条件在实践中都过于计算密集且难以实现。

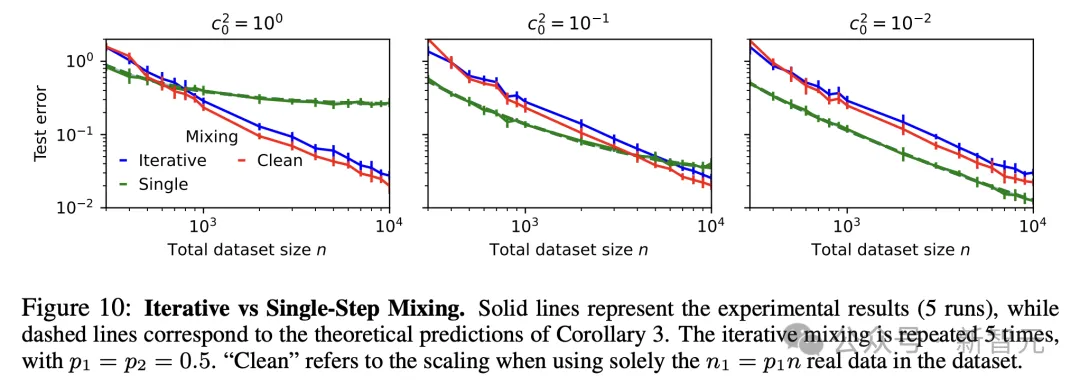
而且，迭代混合主要依赖真实数据。

在图10中，研究人员比较了迭代混合的scaling效果，与仅使用同一训练集中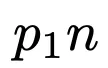部分真实数据（Clean）所获得的scaling效果。

虽然scaling率保持一致，但迭代混合的表现始终不如单独使用真实数据。

这表明迭代混合可能主要是中和了合成数据，并严重依赖真实数据来恢复scaling效果。

即使原始合成数据质量很高（即当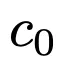很小时，如图10最右侧所示），迭代方法也未能有效利用合成数据，导致性能比单次混合更差。

因此，尽管迭代混合恢复了相同的scaling率，模型仍在某种程度上发生了崩溃，并且没有观察到显著的性能改善。

最后，研究人员还证明了，与少量实际数据进行迭代混合，也是会导致模型崩溃。

总而言之，这项研究系统地描述了真实、合成数据混合，训练模型的效果，表明了模型崩溃是一种稳健的现象，即使在合成数据比例很小的情况下。

作者介绍

Elvis Dohmatob

2021年，Elvis Dohmatob加入了FacebookAI Research（FAIL）成为一名研究员。在此之前，他曾在INRIA、Criteo担任过研究员。

他的研究兴趣包括：深度学习(主要是理论方面)、稳健优化等等。

Yunzhen Feng（冯韫禛）

Yunzhen Feng目前是纽约大学数据科学中心数学和数据组的博士生，导师是Julia Kempe教授。在Meta的FIRE实习期间，与Yann Olivier博士共事。

目前，他的研究兴趣在于：1)改进的科学推理方法，2)强化学习和测试时间优化，3)人工智能合成数据对当代学习范式的影响。

他曾在2021年获得北大数院应用数学学士学位，导师是Bin Dong教授。

Arjun Subramonian

Arjun Subramonian目前是UCLA计算机科学理论博士生，并在Meta实习。

他的博士研究重点是图神经网络中社会不公平的理论基础，对利用谱图理论和统计学来表征图的结构属性如何导致算法不公平感兴趣。

Julia Kempe

Julia Kempe是纽约大学数据科学中心和Courant数学科学研究所计算机科学、数学和数据科学的银牌教授，也是Meta Fair的客座高级研究员。