遇到一个问题用不同表达方式prompt时,大模型往往会给出两种不同的答案。
比如,「秘鲁的首都是什么」,「利马是秘鲁的首都吗」。
对于这种回答不一致的问题,科学家们纷纷为大模型的「智商」担忧起来。
正如了LeCun所言:
LLM确实比狗积累了更多的事实知识和语言能力。但是它们对物理世界的理解能力,以及推理规划能力,远远不及狗。

那么,有没有一种方式,能够解开大模型幻觉,让结果更加准确、高效?
来自MIT的研究人员,将「博弈论」的思想引入大模型的改进中。
他们共同设计了一个游戏,在游戏中,让模型的两种模式(生成式和判别式)相互对抗,努力找到它们可以达成一致的答案。
这个简单的博弈过程,被称为「共识博弈」(CONSENSUS GAME)。
也就是,让模型自我对抗,以提升LLM准确性和内部一致性。

论文地址:https://openreview.net/pdf?id=n9xeGcI4Yg
具体来说,这是一种免训练,基于博弈论的语言模型解码过程。
新方法将语言模型解码,视为一种正则化的不完全信息序列信号博弈游戏——称之为CONSENSUS GAME(共识博弈)。
其中,生成器(GENERATOR)试图使用自然语言句子,向一个判别器(DISCRIMINATOR)传达抽象的正确性参数。
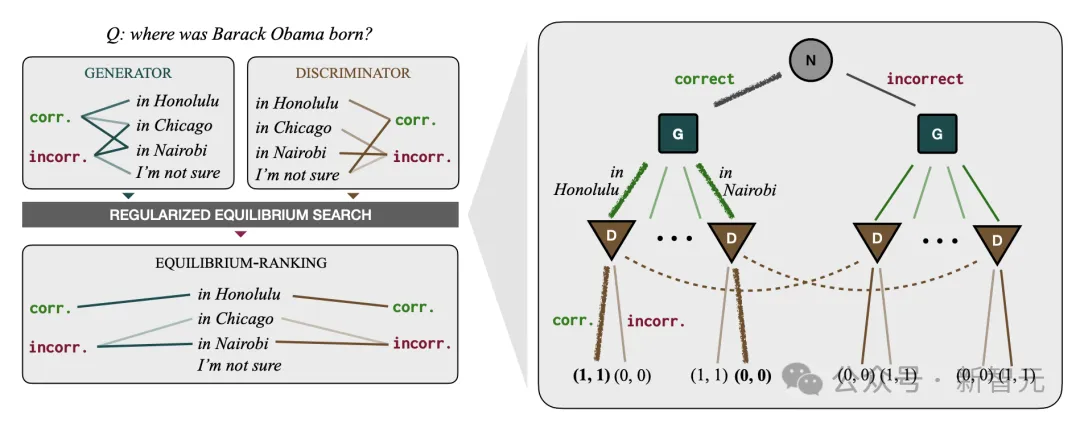
然后,研究人员开发了计算程序,以寻找博弈的近似均衡,从而得到一种名为「均衡排序」(EQUILIBRIUM-RANKING)的解码算法。
在多个基准测试中,「均衡排序」策略在LLaMA-7B的表现中,明显超越LLaMA-65B,并与PaLM540B相媲美。

最新论文已被ICLR 2024接收。

谷歌研究科学家Ahmad Beirami表示,「几十年来,LLM对提示的响应方式一直如出一辙。MIT研究人员提出了将博弈论引入这一过程的新颖想法,开创了一个全新的范式,这有可能带来大量新的应用」。
游戏,不再单纯是衡量AI的标准
以往,通过机器学习在游戏竞赛中的表现,去判断某个AI系统是否取得成功。
而这样的案例,比比皆是。
1997年,IBM深蓝计算机击败了国际象棋特级大师Garry Kasparov,创下了所谓的「思考机器」的里程碑。
19年后,谷歌DeepMind发明的AlphaGo,在围棋比赛中一举战胜李世石。
五局比赛中获胜四局,揭示了人类在某些领域已不再独占鳌头。
不仅如此,AI还在跳棋、双人扑克,以及其他的「零和游戏」中超越了人类。
与以往不同的是,MIT团队而是选择从另一个角度来看问题——用游戏去改进人工智能。
对于AI研究人员来说,一款称为「Diplomacy」的游戏,提出了一个更大的挑战。

由Allan B. Calhamer于1959年设计的经典桌游
与只有2个对手玩家的游戏不同,Diplomacy游戏有7个玩家参与,每个人的动机都很难看透。
要想获胜,玩家必须谈判,缔结合作关系,但不得不提防的是,任何时候任何人都可能遭到背叛。
这款游戏如此复杂,以至于2022年,Meta团队发布的Cicero在40局游戏后,达到「人类水平」时,引发一阵轰动。

论文地址:https://www.science.org/doi/10.1126/science.ade9097
尽管Cicero没能战胜世界冠军,但它在与人类参与者的比赛中进入了前10%,表现足够优秀。
现在,论文作者Athul Paul Jacob是MIT的博士生,曾在Meta实习期间参与了这次研究。
研究期间,Jacob对Cicero依赖语言模型,与其他玩家进行对话的事实感到震惊。
他感受到了,尚未开发出的AI潜力。

Athul Paul Jacob帮助设计了「共识博弈」——为LLM提供了一种提高其准确性和可靠性的方法
于是,他便提出,如果将重点转移到,利用游戏来提高LLM的性能上会怎样?
1000场比赛,让LLM自我对抗
为了追寻这一问题的答案,2023年Jacob与麻省理工学院的Yikang Shen、Gabriele Farina,以及导师Jacob Andreas一起研究,什么可以促进「共识博弈」。
这一思想的核心是,将两个人之间的对话想象成一个合作游戏。
当听者理解说话者想要传达的东西时,就成功了。
尤其是,「共识博弈」的目的是,旨在协调LLM的两个系统——生成器和辨别器。
众所周知,生成器负责处理生成性问题,而辨别器负责处理辨别性问题。
经过几个月的研究,他们终于将这一原则,构建成了一场完整的比赛。
首先,生成器收到一个问题——可以来自人类,也可以来自预存在的名单中,比如「奥巴马出生在哪里」。
然后,生成器会得到一些候选响应,比如火奴鲁鲁(Honolulu)、芝加哥(Chicago)、内罗毕(Nairobi)。
同样,这些响应的选项,可以来自人类、列表,或是由语言模型本身执行搜索。
但在回答之前,生成器会先根据一次公平的随机掷币的结果,被指示生成正确或错误的答复。
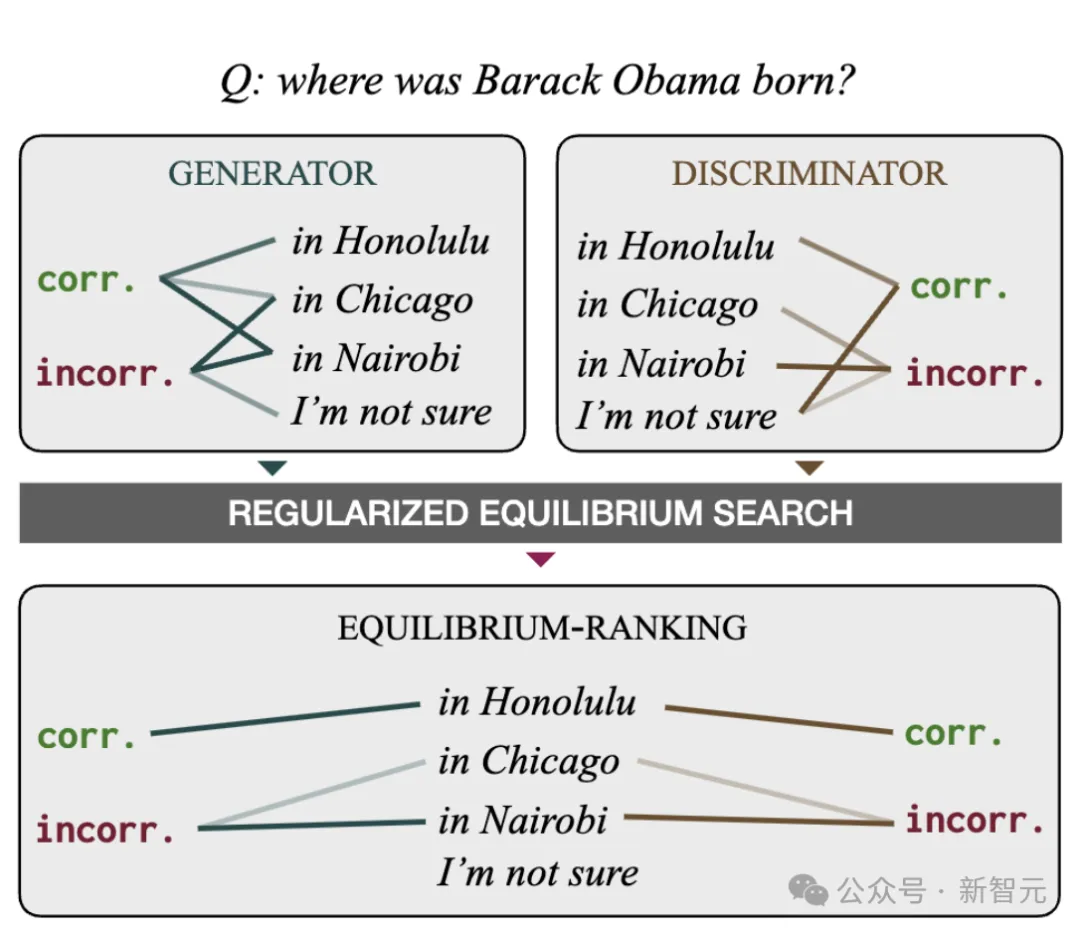
如果结果为正面,那么生成器就会尝试给出正确的答案。
然后,生成器将原始问题,及其选择的回答,一并发送给判别器。
如果判别器判定生成器,是有意地发送了正确的回答,作为一种激励,它们每人得到一分。
而如果结果为反面,生成器就会给出它认为是错误的答案,那判别器看出它故意给了错误答案,它们将在分别得到一分。
这就体现了策略的核心点,即通过激励,让它们达成一致。
在这个博弈过程开始时,生成器和判别器都有自己对答案的「先验信念」。
这些「信念」以概率分布的形式体现,比如,生成器基于从互联网获取的信息,可能会认为:
奥巴马出生在火奴鲁鲁的概率是80%,芝加哥10%,内罗毕5%,其他地方5%。
当然判别器,也会有不同概率分布的「先验信念」。
虽然两个「玩家」会因达成一致而获得奖励,但如果偏离自己「先验信念」太多时,也会被扣分。
这样一来,可以鼓励「玩家」将从互联网获取的知识,融入到回答中,从而让模型更加准确。
如果没有这种机制,它们可能会就一个完全错误的答案(如Delhi)上达成一致,却仍然获得分数。
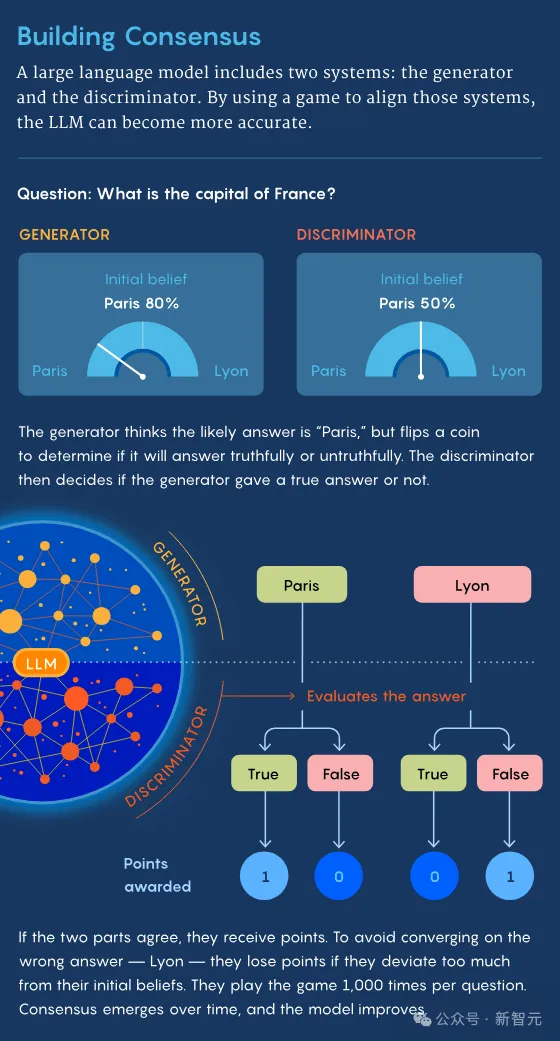
对于每个问题,这两个系统相互之间进行了大约1000场比赛。
在无数次迭代的过程中,双方都了解了对方的「信念」,并相应地修改了自己的战略。
最终,生成器和判别器开始达成更多共识,因为它们逐渐进入了一种称为「纳什均衡」(Nash equilibrium)的状态。
这可以说是博弈论的核心概念。
「纳什均衡」代表了游戏中的一种平衡状态,在这点上,任何玩家都无法通过改变策略,来改善个人结果。
比如,在石头剪刀布游戏中,当玩家选择三个选项的概率正好都是1/3时,才能获得最佳结果,任何其他策略都会导致更糟糕的结果。
在「共识博弈」中,「纳什均衡」可以通过多种方式实现。
比如,判别器可能会观察到,每当生成器将奥巴马的出生地回答为「火奴鲁鲁」时,它就会得分。
经过多轮博弈,生成器和判别器会学习到,继续这种作答方式会得到奖励,而没有动机改变策略。
这种一致的作答方式,就代表了对于该问题的一种可能的「纳什均衡」。
70B参数Llama,媲美5400亿参数PaLM
除此之外,还可能存在其他「纳什均衡」的解。
MIT团队还依赖于一种改进的「纳什均衡」形式,结合了玩家们的「先验信念」,有助于让回答结果更加贴近现实。
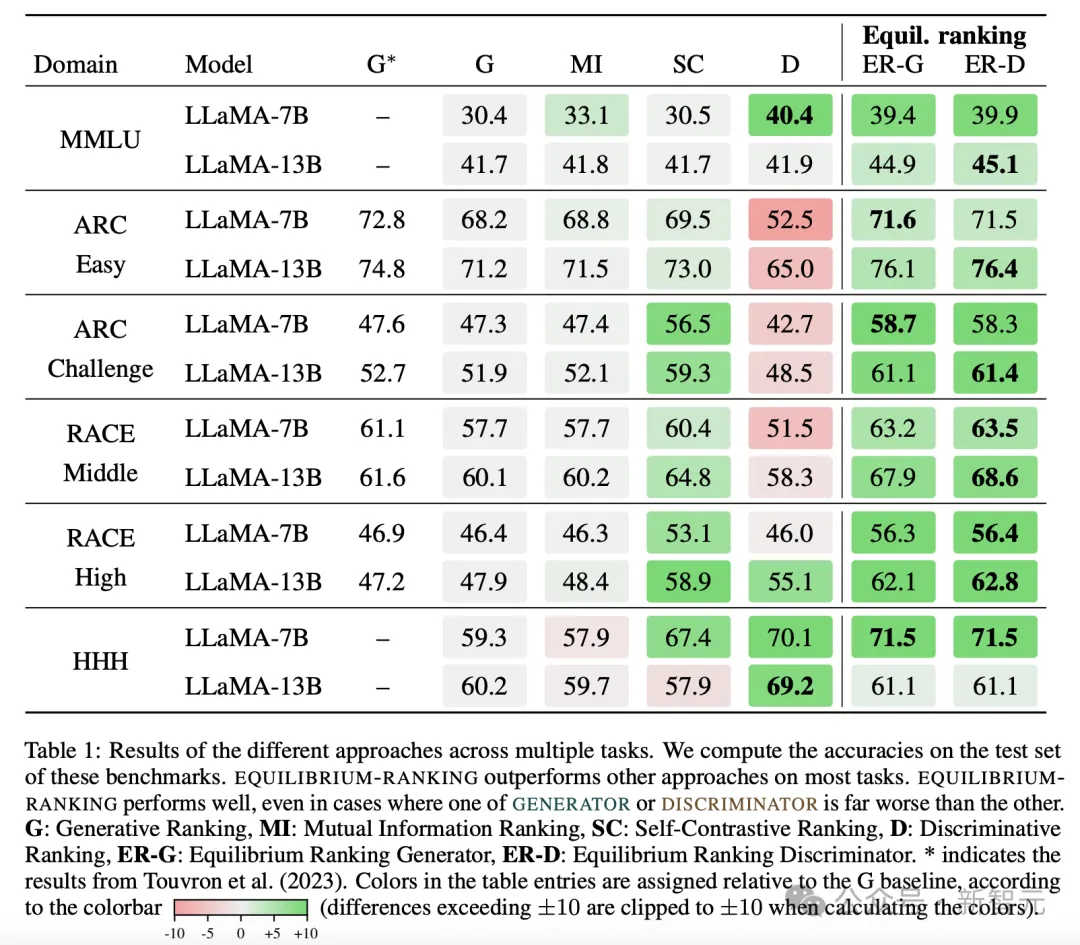
为了测试「共识博弈」的效果,研究团队在一些中等参数规模的语言模型(70亿-130亿参数)上进行了一系列标准问题测试。
经过训练后的这些模型,正确答案的比例明显高于未经训练的模型,甚至高于一些拥有高达5400亿参数的大型模型PaLM。
这不仅提高了模型的答案准确性,也增强了模型的内部一致性。
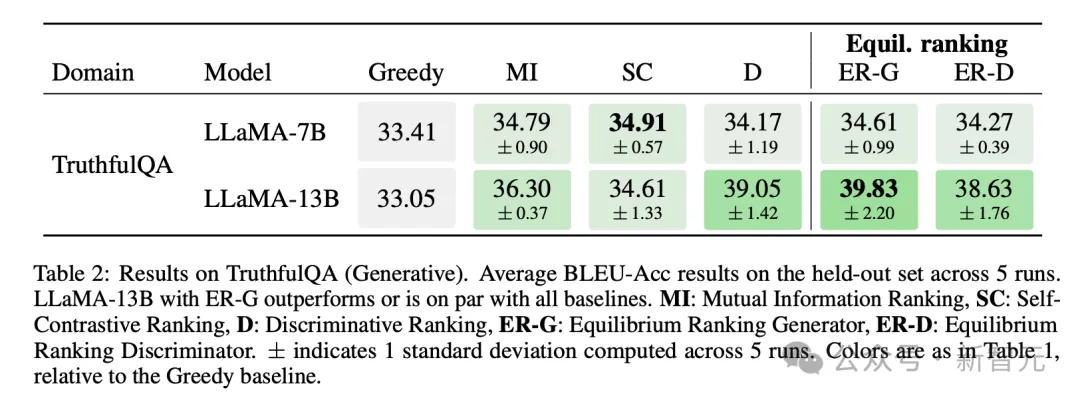
另外,在TruthfulQA(生成)的结果上,具有ER-G的LLaMA-13B优于或与所有基线持平。
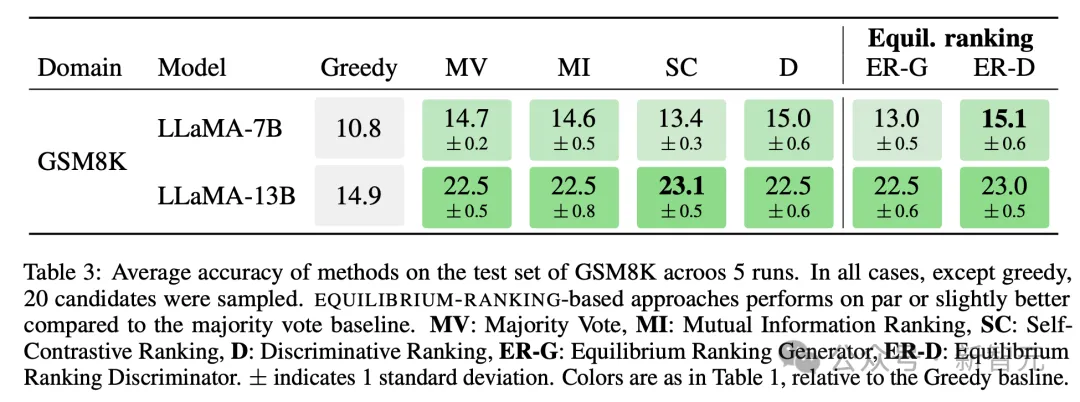
研究人员在GSM8K测试集上,对不同方法的平均准确率进行了评估和对比。
除了greedy外,都是对20个候选回答进行了采样。
基于「均衡排序」的方法,其性能与多数投票基线相当,或者稍微好一些。
一般来说,任何LLM都可以通过与自身进行「共识博弈」从中获益。
最重要的是,研究人员成,只需在一台笔记本上,进行的1000轮「共识博弈」仅需几毫秒的时间,计算代价很小。
Omidshafiei表示,「这种方法非常高效,不需要对基础语言模型进行训练或修改」。
下一步,大小模型一起游戏
在「共识博弈」取得初步成功后,Jacob现在正在探索将博弈论,应用到LLM研究中的其他方式。
在这个基础上,他现在又提出了一种新的方法,暂称为「集成博弈」(ensemble game)。
在「集成博弈」中,有一个主模型(primary LLM),与若干个小型模型进行博弈互动。
这些小型模型中,至少有一个扮演「盟友」角色,至少有一个扮演「对手」角色。
问题出现时,比如法国首都是什么,如果主模型与「盟友」模型给出相同答案,主模型会获得分数。
如果与「对手」模型给出不同答案,也会获得分数。
通过这种与小模型的博弈互动,并不需要对主模型进行额外训练或改变参数,就可以进一步提升主模型的性能表现。
这种将大模型与多个小模型集成互动的新范式,让大模型可以借鉴小模型的优点。
同时还能相互制约,从而提高整体的准确性和一致性。
在未来,它将为提升LLM性能开辟了一种全新的思路和方法。






还没有评论,来说两句吧...