时间序列预测是一个经久不衰的主题,受自然语言处理领域的成功启发,transformer模型也在时间序列预测有了很大的发展。本文可以作为学习使用Transformer 模型的时间序列预测的一个起点。
数据集 这里我们直接使用kaggle中的 Store Sales — Time Series Forecasting作为数据。这个比赛需要预测54家商店中各种产品系列未来16天的销售情况,总共创建1782个时间序列。数据从2013年1月1日至2017年8月15日,目标是预测接下来16天的销售情况。虽然为了简洁起见,我们做了简化处理,作为模型的输入包含20列中的3,029,400条数据,。每行的关键列为' store_nbr '、' family '和' date '。数据分为三类变量:
1、截止到最后一次训练数据日期(2017年8月15日)之前已知的与时间相关的变量。这些变量包括数字变量,如“销售额”,表示某一产品系列在某家商店的销售额;“transactions”,一家商店的交易总数;' store_sales ',该商店的总销售额;' family_sales '表示该产品系列的总销售额。
2、训练截止日期(2017年8月31日)之前已知,包括“onpromotion”(产品系列中促销产品的数量)和“dcoilwtico”等变量。这些数字列由' holiday '列补充,它表示假日或事件的存在,并被分类编码为整数。此外,' time_idx '、' week_day '、' month_day '、' month '和' year '列提供时间上下文,也编码为整数。虽然我们的模型是只有编码器的,但已经添加了16天移动值“onpromotion”和“dcoilwtico”,以便在没有解码器的情况下包含未来的信息。
3、静态协变量随着时间的推移保持不变,包括诸如“store_nbr”、“family”等标识符,以及“city”、“state”、“type”和“cluster”等分类变量(详细说明了商店的特征),所有这些变量都是整数编码的。
我们最后生成的df名为' data_all ',结构如下:
在将数据转换为适合我的PyTorch模型的张量之前,需要将其分为训练集和验证集。窗口大小是一个重要的超参数,表示每个训练样本的序列长度。此外,' num_val '表示使用的验证折数,在此上下文中设置为2。将2013年1月1日至2017年6月28日的观测数据指定为训练数据集,以2017年6月29日至2017年7月14日和2017年7月15日至2017年7月30日作为验证区间。
同时还进行了数据的缩放,完整代码如下:
数据加载器 在数据加载时,需要将每个时间序列从窗口范围内的随机索引开始划分为时间块,以确保模型暴露于不同的序列段。
为了减少偏差还引入了一个额外的超参数设置,它不是随机打乱数据,而是根据块的开始时间对数据集进行排序。然后数据被分成五部分——反映了我们五年的数据集——每一部分都是内部打乱的,这样最后一批数据将包括去年的观察结果,但还是随机的。模型的最终梯度更新受到最近一年的影响,理论上可以改善最近时期的预测。
复制 def divide_shuffle(df,div_num):
space = df.shape[0]//div_num
division = np.arange(0,df.shape[0],space)
return pd.concat([df.iloc[division[i]:division[i]+space,:].sample(frac=1) for i in range(len(division))])
def create_time_blocks(time_length,window_size):
start_idx = np.random.randint(0,window_size-1)
end_idx = time_length-window_size-16-1
time_indices = np.arange(start_idx,end_idx+1,window_size)[:-1]
time_indices = np.append(time_indices,end_idx)
return time_indices
def data_loader(x_numeric_tensor, x_category_tensor, x_static_tensor, y_tensor, batch_size, time_shuffle):
num_series = x_numeric_tensor.shape[0]
time_length = x_numeric_tensor.shape[1]
index_pd = pd.DataFrame({'serie_idx':range(num_series)})
index_pd['time_idx'] = [create_time_blocks(time_length,window_size) for n in range(index_pd.shape[0])]
if time_shuffle:
index_pd = index_pd.explode('time_idx')
index_pd = index_pd.sample(frac=1)
else:
index_pd = index_pd.explode('time_idx').sort_values('time_idx')
index_pd = divide_shuffle(index_pd,5)
indices = np.array(index_pd).astype(int)
for batch_idx in np.arange(0,indices.shape[0],batch_size):
cur_indices = indices[batch_idx:batch_idx+batch_size,:]
x_numeric = torch.stack([x_numeric_tensor[n[0],n[1]:n[1]+window_size,:] for n in cur_indices])
x_category = torch.stack([x_category_tensor[n[0],n[1]:n[1]+window_size,:] for n in cur_indices])
x_static = torch.stack([x_static_tensor[n[0],:] for n in cur_indices])
y = torch.stack([y_tensor[n[0],n[1]+window_size:n[1]+window_size+forecast_length] for n in cur_indices])
yield x_numeric.to(device), x_category.to(device), x_static.to(device), y.to(device)
def val_loader(x_numeric_tensor, x_category_tensor, x_static_tensor, y_tensor, batch_size, num_val):
num_time_series = x_numeric_tensor.shape[0]
for i in range(num_val):
for batch_idx in np.arange(0,num_time_series,batch_size):
x_numeric = x_numeric_tensor[batch_idx:batch_idx+batch_size,window_size*i:window_size*(i+1),:]
x_category = x_category_tensor[batch_idx:batch_idx+batch_size,window_size*i:window_size*(i+1),:]
x_static = x_static_tensor[batch_idx:batch_idx+batch_size]
y_val = y_tensor[batch_idx:batch_idx+batch_size,window_size*(i+1):window_size*(i+1)+forecast_length]
yield x_numeric.to(device), x_category.to(device), x_static.to(device), y_val.to(device)1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.
模型 我们这里通过Pytorch来简单的实现《Attention is All You Need》(2017)²中描述的Transformer架构。因为是时间序列预测,所以注意力机制中不需要因果关系,也就是没有对注意块应用进行遮蔽。
从输入开始:分类特征通过嵌入层传递,以密集的形式表示它们,然后送到Transformer块。多层感知器(MLP)接受最终编码输入来产生预测。嵌入维数、每个Transformer块中的注意头数和dropout概率是模型的主要超参数。堆叠多个Transformer块由' num_blocks '超参数控制。
下面是单个Transformer块的实现和整体预测模型:
复制 class transformer_block(nn.Module):
def __init__(self,embed_size,num_heads):
super(transformer_block, self).__init__()
self.attention = nn.MultiheadAttention(embed_size, num_heads, batch_first=True)
self.fc = nn.Sequential(nn.Linear(embed_size, 4 * embed_size),
nn.LeakyReLU(),
nn.Linear(4 * embed_size, embed_size))
self.dropout = nn.Dropout(drop_prob)
self.ln1 = nn.LayerNorm(embed_size, eps=1e-6)
self.ln2 = nn.LayerNorm(embed_size, eps=1e-6)
def forward(self, x):
attn_out, _ = self.attention(x, x, x, need_weights=False)
x = x + self.dropout(attn_out)
x = self.ln1(x)
fc_out = self.fc(x)
x = x + self.dropout(fc_out)
x = self.ln2(x)
return x
class transformer_forecaster(nn.Module):
def __init__(self,embed_size,num_heads,num_blocks):
super(transformer_forecaster, self).__init__()
num_len = len(numeric_covariates)
self.embedding_cov = nn.ModuleList([nn.Embedding(n,embed_size-num_len) for n in categorical_covariates_num_embeddings])
self.embedding_static = nn.ModuleList([nn.Embedding(n,embed_size-num_len) for n in categorical_static_num_embeddings])
self.blocks = nn.ModuleList([transformer_block(embed_size,num_heads) for n in range(num_blocks)])
self.forecast_head = nn.Sequential(nn.Linear(embed_size, embed_size*2),
nn.LeakyReLU(),
nn.Dropout(drop_prob),
nn.Linear(embed_size*2, embed_size*4),
nn.LeakyReLU(),
nn.Linear(embed_size*4, forecast_length),
nn.ReLU())
def forward(self, x_numeric, x_category, x_static):
tmp_list = []
for i,embed_layer in enumerate(self.embedding_static):
tmp_list.append(embed_layer(x_static[:,i]))
categroical_static_embeddings = torch.stack(tmp_list).mean(dim=0).unsqueeze(1)
tmp_list = []
for i,embed_layer in enumerate(self.embedding_cov):
tmp_list.append(embed_layer(x_category[:,:,i]))
categroical_covariates_embeddings = torch.stack(tmp_list).mean(dim=0)
T = categroical_covariates_embeddings.shape[1]
embed_out = (categroical_covariates_embeddings + categroical_static_embeddings.repeat(1,T,1))/2
x = torch.concat((x_numeric,embed_out),dim=-1)
for block in self.blocks:
x = block(x)
x = x.mean(dim=1)
x = self.forecast_head(x)
return x1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.
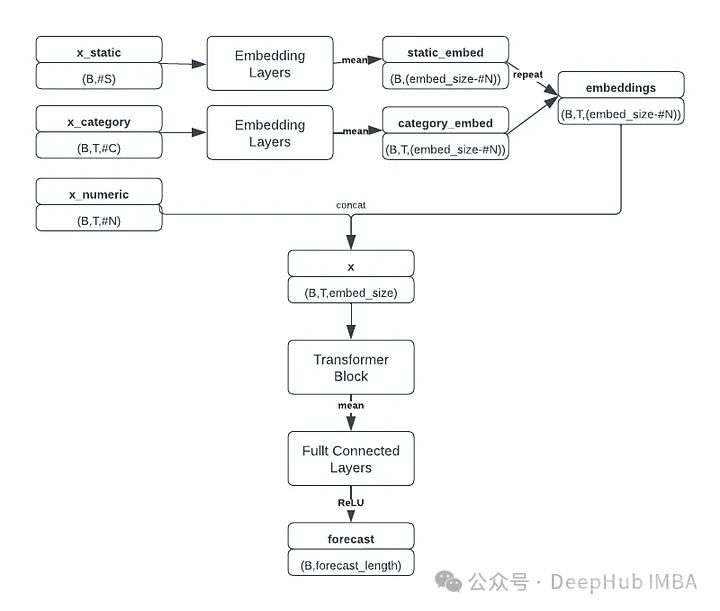
我们修改后的transformer架构如下图所示:
模型接受三个独立的输入张量:数值特征、分类特征和静态特征。对分类和静态特征嵌入进行平均,并与数字特征组合形成具有形状(batch_size, window_size, embedding_size)的张量,为Transformer块做好准备。这个复合张量还包含嵌入的时间变量,提供必要的位置信息。
Transformer块提取顺序信息,然后将结果张量沿着时间维度聚合,将其传递到MLP中以生成最终预测(batch_size, forecast_length)。这个比赛采用均方根对数误差(RMSLE)作为评价指标,公式为:
鉴于预测经过对数转换,预测低于-1的负销售额(这会导致未定义的错误)需要进行处理,所以为了避免负的销售预测和由此产生的NaN损失值,在MLP层以后增加了一层ReLU激活确保非负预测。
训练和验证 训练模型时需要设置几个超参数:窗口大小、是否打乱时间、嵌入大小、头部数量、块数量、dropout、批大小和学习率。以下配置是有效的,但不保证是最好的:
这里使用adam优化器和学习率调度,以便在训练期间逐步调整学习率。
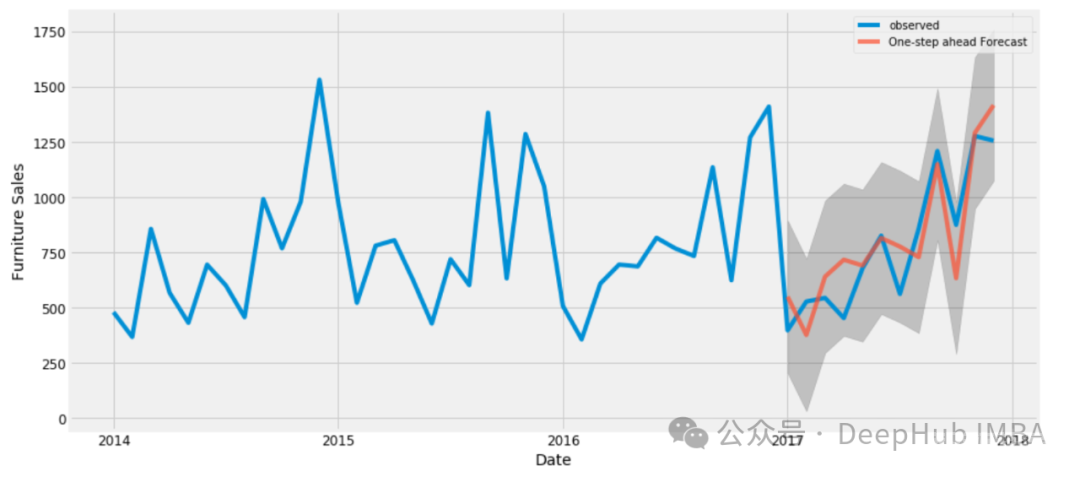
结果 训练后,表现最好的模型的训练损失为0.387,验证损失为0.457。当应用于测试集时,该模型的RMSLE为0.416,比赛排名为第89位(前10%)。
更大的嵌入和更多的注意力头似乎可以提高性能,但最好的结果是用一个单独的Transformer 实现的,这表明在有限的数据下,简单是优点。当放弃整体打乱而选择局部打乱时,效果有所改善;引入轻微的时间偏差提高了预测的准确性。
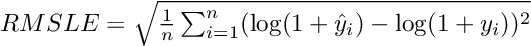






还没有评论,来说两句吧...